Defines functions to perform spectral bisection. More...
Go to the source code of this file.
Functions | |
| std::vector< int > | spectralBisection (Graph G) |
| Performs spectral bisection on a graph. More... | |
| std::vector< int > | getIndexMap (std::vector< double > Eigvec2) |
| Gets the index map for the reordered graph. More... | |
Defines functions to perform spectral bisection.
The main computation in solving the page rank problem reduces to a matrix vector multiplication. For large data sets, the problem can be solved more efficeitnly by performing the matvecs in parallel. However, any part of the matvec operation cooresponding to data in the off-diagonal blocks of the matrix requires between node/processor communication. This is shown in the following figure where there are 4 processors in total.
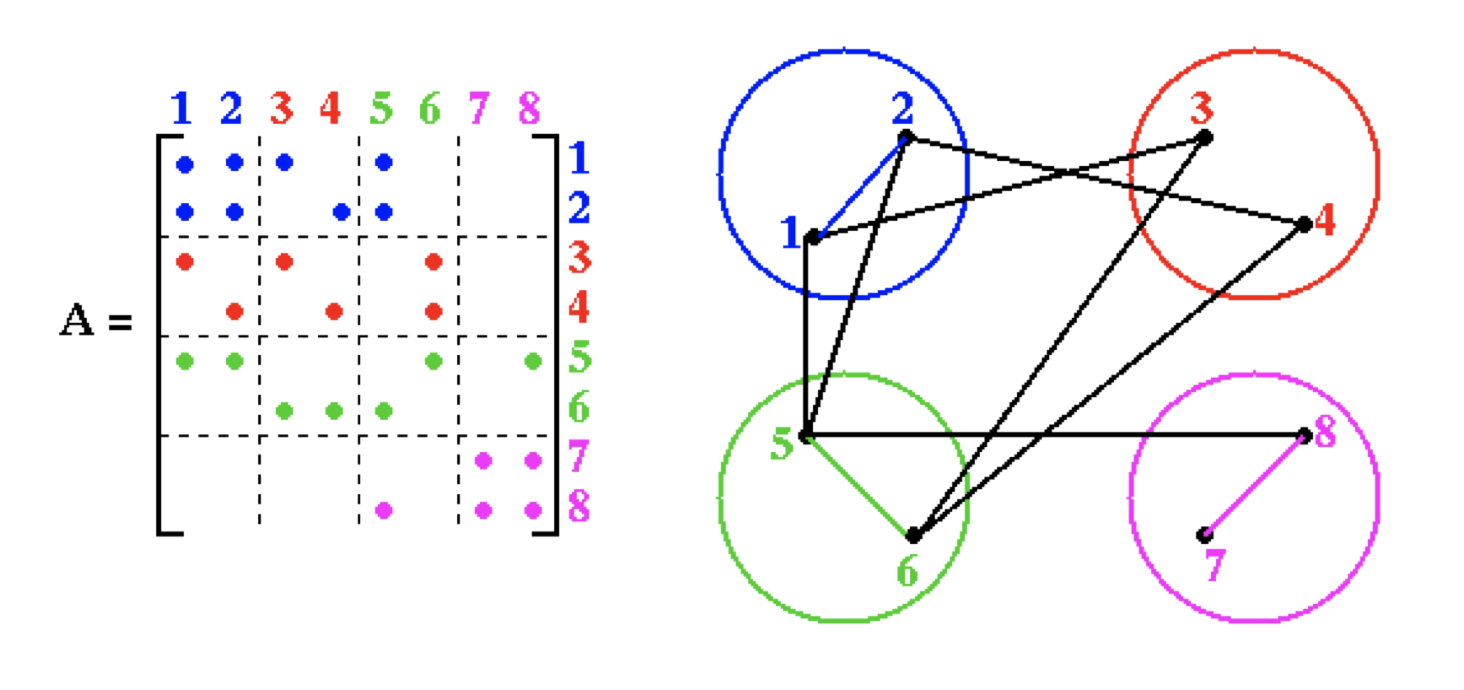
Clearly the cost of the matvec will be proportional to the number of edges across processors. If the matrix is sparse, we can reduce the amount of communication by reordering the matrix before the matvec in a way that reduces the number of off diagonal entries. For relatively small data sets, spectral bisection can be used to determine this reordered. The steps of spectral bisection include
An example of this process is shown below.
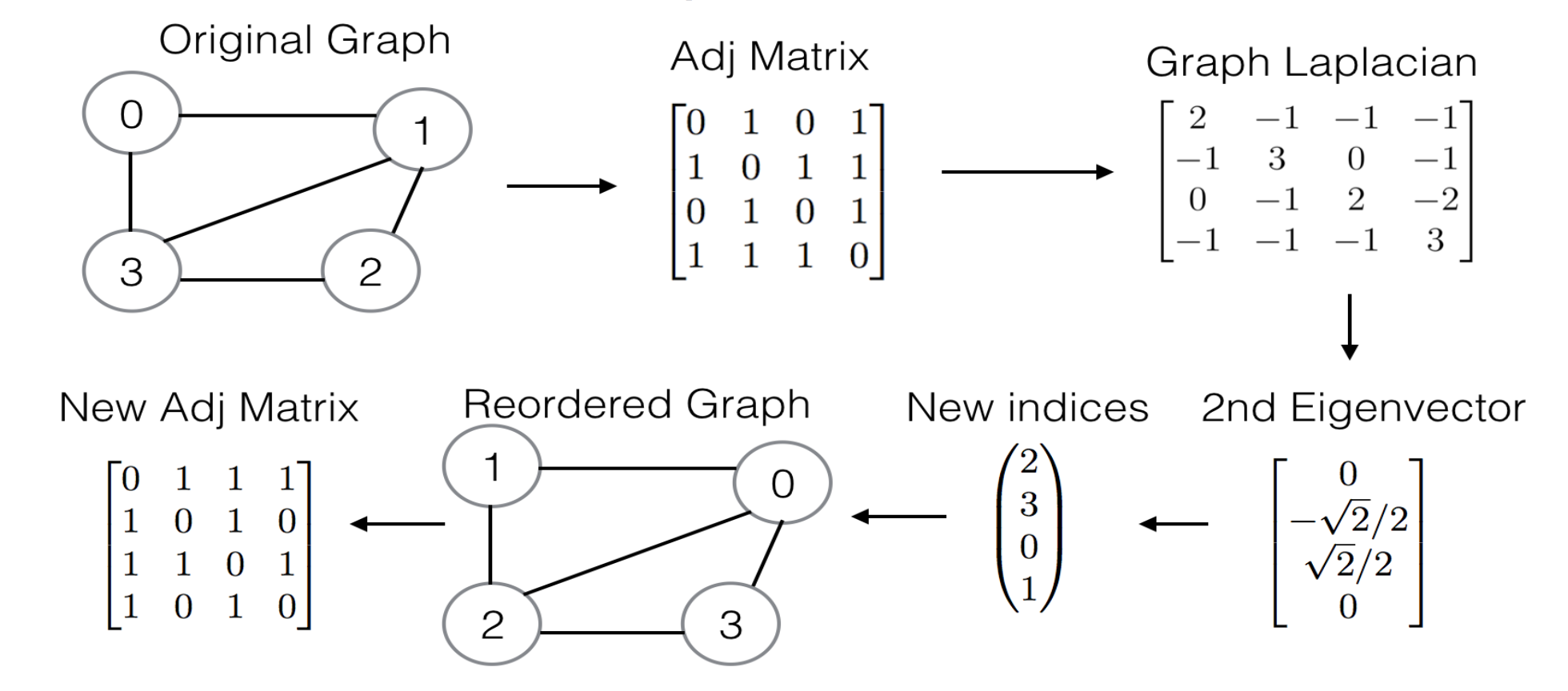
Arnoldi iteration is used to compute the second smallest eigenvalue (through ARPACK). For larger datasets, this process is too expensive and so the matrix must first be coarsened before applying spectral bisection. See coarsen.h for more information on the coarsening process.
| std::vector<int> getIndexMap | ( | std::vector< double > | Eigvec2 | ) |
Gets the index map for the reordered graph.
| Eigvec2 | Vector cooresponding to the second eigenvalue |