copyright@planets_for

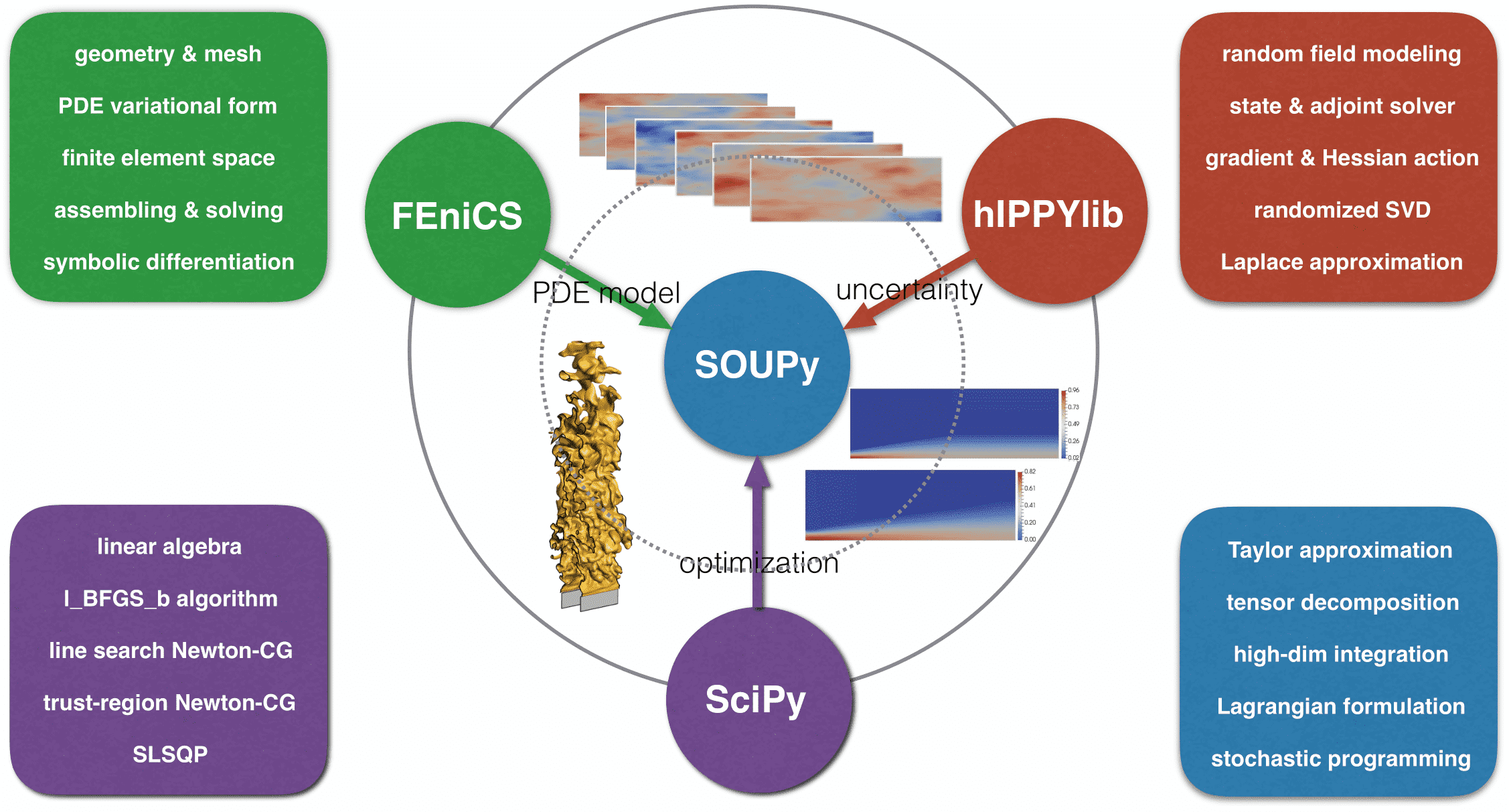
SOUPy implements scalable algorithms to solve problems of PDE-constrained optimization under uncertainty, with the computational complexity measured in terms of PDE solves independent of the uncertain parameter dimension and optimization variable dimension. SOUPy is built on the open-source hIPPYlib library, which provides state-of-the-art scalable adjoint-based methods for deterministic and Bayesian inverse problems governed by PDEs, which in turn makes use of the FEniCS library for high-level formulation, discretization, and scalable solution of PDEs.
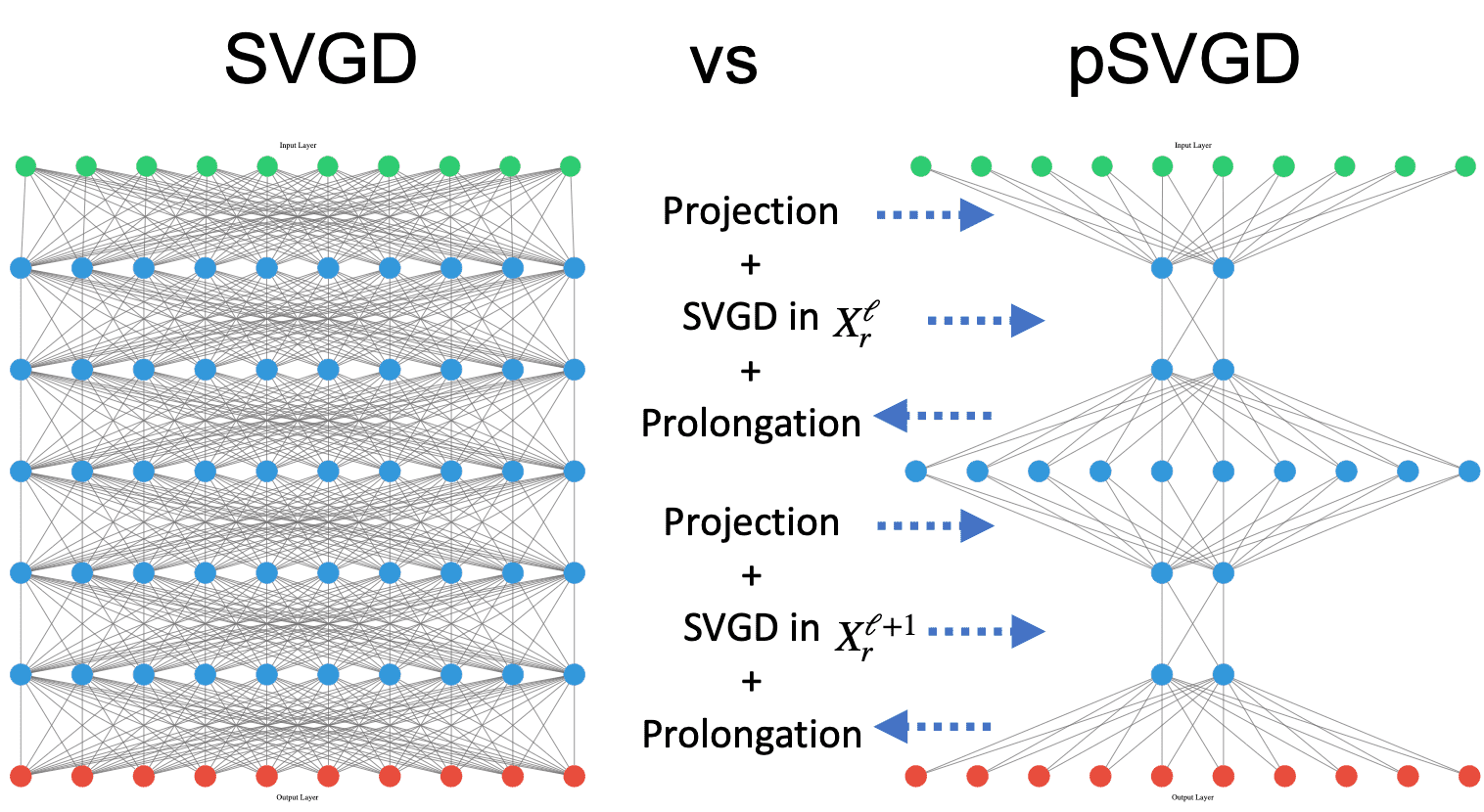
pSVGD implements scalable projection-based Stein variational inference algorithms to solve model-constrained (both PDE models and other models) Bayesian inverse problems with high/infinite-dimensional random parameter field/process. The library also includes implementation of projected Stein variational Newton (pSVN) method and with extension to projected Wasserstein gradient descent (pWGD) method.
Model reduction is known very challenging for high-dimensional parametric problems whose solutions also live in high-dimensional manifolds. However, often the manifold of some quantity of interest (QoI) depending on the parametric solutions is low-dimensional. LearnROM implements structure-exploiting algorithms to efficiently learn the intrinsic parameter subspace in which the QoI is most sensitive. Both the gradient-based active subspace and Hessian-based subspace are implemented in LearnROM. Samples are drawn from such subspaces to learn the QoI-oriented ROM.
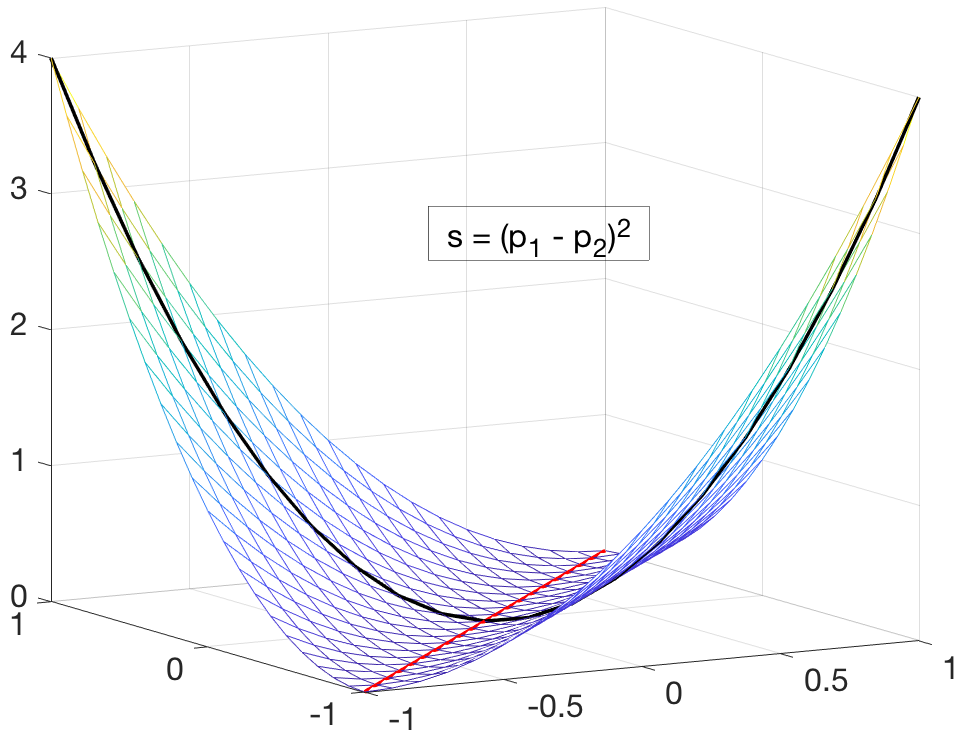

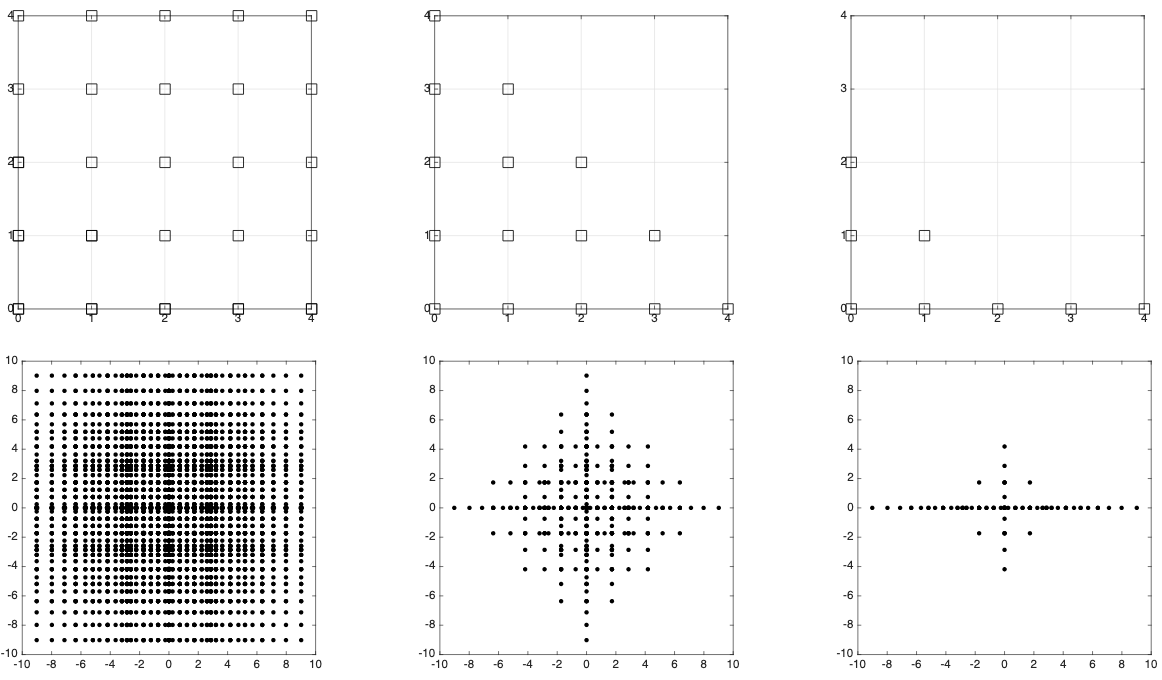
This MATLAB library implements sparse quadrature rule for high-dimensional integration with Gaussian measures. It provides both a-priori (integrand-independent) and a-posteriori (integrand-dependent) construction algorithms to push the integration to very high dimensions (up to 10,000 dimensions tested). Depending on the sparsity of the integrand, it can achieve dimension-independent convergence rates and faster convergence than Monte Carlo for high-dimensional integration problems.
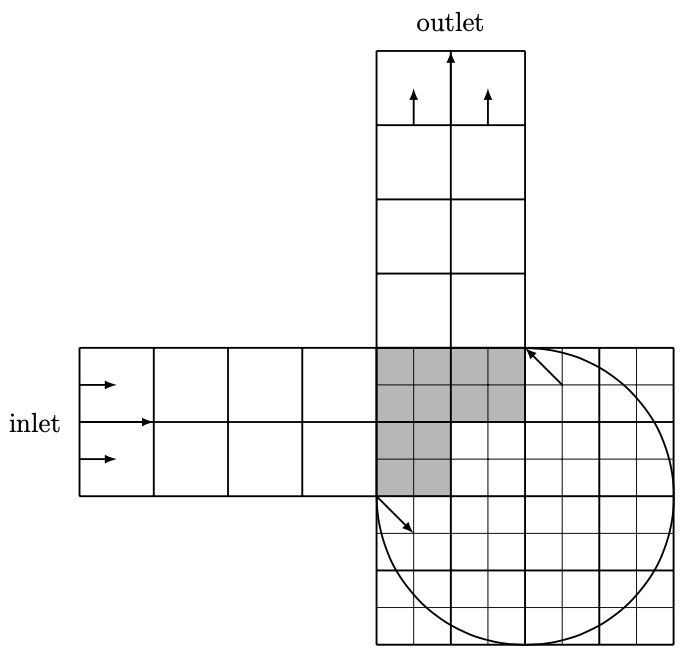
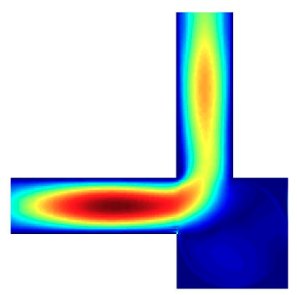
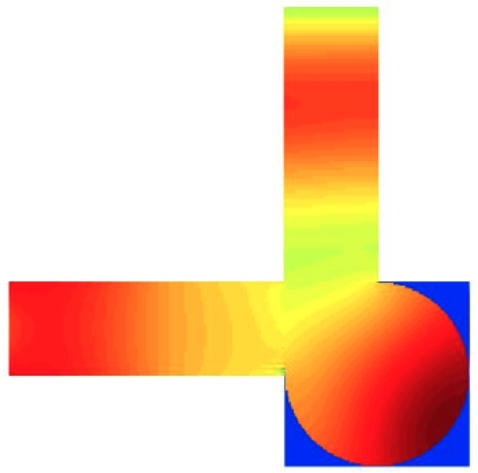
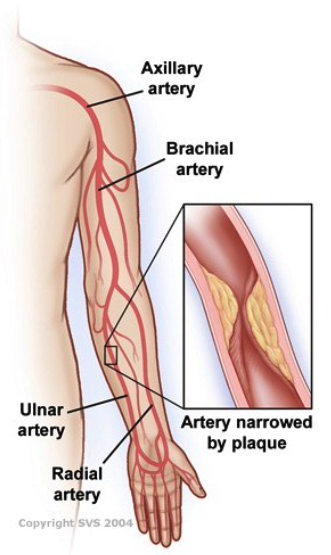
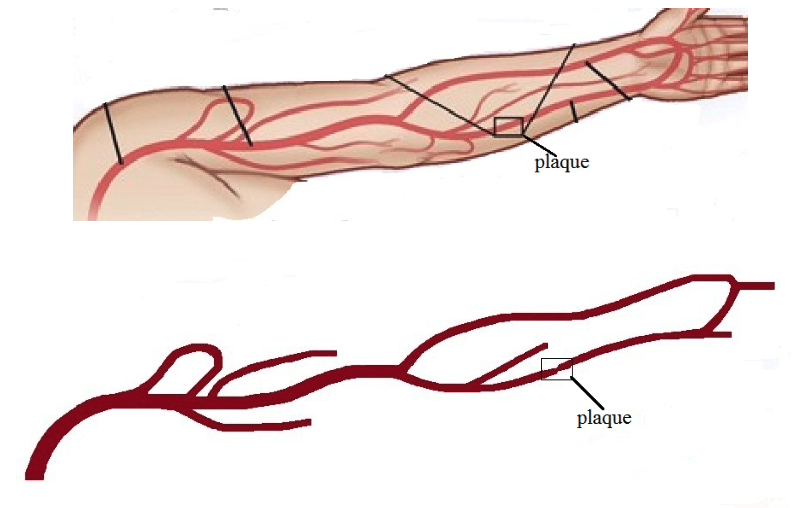
This MATLAB library implements the examples of lattice Boltzmann methods in the thesis The Lattice Boltzmann Method for Fluid Dynamics: Theory and Applications, which includes Poiseuille flow, lid driven cavity flow, Womersley flow, Taylor-Couette flow, blood flow in aneurysms, etc. This library also implements the most common schemes for imposing boundary conditions on both straight and curved boundaries. In particular, it features multiblock and multigrid implementation that enables the lattice Boltzmann methods to more practical applications in complex geometries, as shown in the following examples of blood flow (velocity and pressure) in cerebral aneurysms and artery with narrowed plaque.